Victoria over at Unschooling Math wrote a post called, “Many Paths to an Endpoint” regarding her discovery about the differences between learning math as a right-brained dominant person and a left-brained dominant person, inspired from my post here. Instead of leaving a lengthy comment, her questions about how each of the math minds fit into the learning process prompted me to write this post.
Victoria starts off her post remembering her days in a university geometry class required for all math teacher majors. This professor taught using big picture concepts and ideas about math and helped his students apply that knowledge to learning about math. Victoria noticed that students either loved or hated the professor. At the time, she wasn’t sure why.
It reminds me of my high school algebra class. I had “always been good at math” since elementary, so although this level math wasn’t required, I took it because I felt I should continue to develop my “math talent.” What I remember most was this young, new math teacher, who was so excited to share his love of math with high school students. He taught math totally different than anyone up to that point. He was teaching concepts and application, and encouraging us to apply math formulas to reach the answer. I remember constantly thinking, “Why won’t he just give us the plain, straight-up math problems that I can plug certain formulas into? I can do those easy-peasy.” Unfortunately, I can’t tell you how I coped because I eventually flunked out due to my inability to stay awake to learn because the math class was first period, and I just couldn’t get myself not to fall asleep almost daily (teen sleep deprivation being a whole other topic in school). It was SO frustrating! It was my only class I ever flunked (I was typically an A/B student).
So, what was going on in these two higher level math class examples? I believe it was the clash that occurs when a left-brained arithmetic person meets a mathematics-centered class. Mathematics is the concept and ideas of numbers 
and patterns. Arithmetic is manipulating numbers. I was great at manipulating numbers! It’s neat and precise and organized and logical. I eventually understood the concept of what addition, subtraction, multiplication and division constituted, but as it pertained to algebra or geometry, I had no clue why I was learning these things or what real life application any of it entailed. Frankly, I still don’t. If I never learned the concepts or application behind the formulas, not making it through higher level math well was inevitable.
Right-brained people are more natural with mathematics, if it’s an area of natural interest or talent. Left-brained people are more natural with arithmetic, if it’s an area of natural interest or talent. I barely scraped a C grade in geometry. With its shapes, space, theorems, and concepts, geometry is best suited for right-brained learners. With its processes, formulas, and multi-steps, algebra is best suited for left-brained learners. As a strong left-brained learner, I enjoyed algebra, and disliked geometry. My builder son, who is natural at and enjoyed math at a young age, came home from a physics class at the community college declaring, “It’s applied math!” He proceeded to sit down with his textbook after the first day in class and spent 3 to 4 hours just playing with the ideas of math through physics. It’s why this same child is choosing to go into computer programming; it’s patterns and math application.
In my post about math that Victoria referenced above, I mention that there are two types of right-brained math minds: visual-based and kinesthetic-based. Victoria was surprised to hear me say this because she thought all students would prefer a visual or kinesthetic approach to learning. This isn’t true, necessarily. My writer daughter interacted with math in a left-brained manner. I 
became so used to presenting math in a right-brained manner, that when she would come to me requesting help, I often would start with some kind of visual, such as, “Well, let’s pretend it’s a pizza (or pie).” She would run from the room, screaming, “No, not the pizza!” She would then go to her father, who would give it to her straight up, plug in the formula, don’t worry about understanding it, and off she would go, happy to complete her math. I was the same way; don’t hurt my brain making me understand the concepts behind it. Just let me do the problems, get the right answer, and receive my A. Isn’t that what we’re taught is the most important thing in school? The right answer and the A?
And, thus, here lies our dilemma. As Victoria began to teach math in school, she was running into the same percentage of students who either loved her presentation of math, or hated it. Some could grasp it; some couldn’t. Victoria’s question then becomes:
I wonder how it would look for a classroom to simultaneously support both sequences of learning.
And Victoria’s subsequent criteria:
I am still convinced that both “arithmetic” and “mathematics” must be supported within a child, even in the early years.
I agree that one would want to expose students to both arithmetic and mathematics in the early years, otherwise, how else can one figure out which is preferred? However, I also strongly encourage supporting our different learners in the way they best would learn math. I share what the right-brained math path 
and left-brained math path look like at my previous math post. As each brain dominant preference works its way through how it assimilates information, each should be honored. I share in my developmental time frame post how the early years of 5 to 7 is for feeding your brain dominant preference in learning, the 8 to 10 year time frame is 
for beginning to transition into learning the less dominant brain strengths, and the 11 to 13 year time frame is for fully integrating both sides of the brain. We can’t force a left-brained dominant person to do better in concepts (I hated word problems!) before the appropriate developmental time, and you can’t force a right-brained dominant person to do better with math facts before the appropriate developmental time, at least without a lot of math angst.
What would need to change in order to honor both math minds? We need to change how we assess learning from testing to portfolios. And we need to change from a standardized education to a strengths-based education. When we use testing as our primary way to assess, we tend to use measurable tasks. At this time, if a right-brained child takes a standardized test and does poorly in the math facts section, but well in the concepts section, it will be expected that he put in more work in math facts in order to be “even” with the standard. Instead, with a strengths-based education, the right-brained learner will get to expand his ability with math concepts while continuing to be exposed to math facts. A lack of development in one area won’t prevent his continued progression in another. In his portfolio, the write-up will acknowledge his strengths and how he is building on those, and note where he is at in developing his math facts. Like a pediatrician’s office, he may be put on a chart showing right-brained and left-brained attributes, where he would fall more heavily on the right-brained side of the chart. In this way, it would be noted that his development is progressing normally for a right-brained learner. Specific notes may appear such as the student preferring mental math processes for his concept work, and that he uses his fingers for math facts. This gives a lot more information.
All of this said, I’m not a believer in all people being proficient in both right- and left-brained specialties. If the brain were able to be standardized, or equalized, which I don’t think it can or should, we would lose what those who are strongly right-brained or strongly left-brained bring to the table. So, let’s take that same right-brained math learner above, and say that by the time he’s 14, he’s integrated many of the math fact skills, though he may still consistently make “mental errors.” Or maybe he chooses to use a calculator. Does that have to be bad? Or what if he decides, as most people will, that math isn’t his field of choice, and he drops math after first level algebra and geometry? He pursues his manga artist career and hires an accountant. Isn’t that sensible? The good news about honoring the natural developmental process for both math minds is that those who truly have an interest or gift in the subject will still have a positive relationship with math in their later years and will bring to the math field all that will benefit our world. We won’t lose great mathematicians (which tends to be right-brained learners) along the way from a mismatched early math learning environment that doesn’t honor their natural path to math development.
I repeat Victoria’s question, I wonder how it would look for a classroom to simultaneously support both sequences of learning? It would be an exciting day for both minds, in math, or any other subject! This is at the heart of education reform that I will continue to fight for through writing about understanding and honoring the natural learning path for right-brained children.
Question: What math attributes have you noticed in your right-brained learner that shows a math mind, or what processes have you noticed that make it difficult for you to honor their particular math developmental path to learning?
OR
What do you think it would look like to support both math minds in the classroom setting?
This is more a response to the question of what a classroom would look like were it to support both sequences of learning.
One model might be the elementary math classrooms in Japan. From what I’ve read, lessons are carefully developed by the teachers themselves — who incidentally have amazing numbers of hours per week to devote to this kind of development — to begin with a problem or situation. This is often a physical/visual problem, such as which of a line-up of differently shaped containers might hold the most liquid, and how one would find out and measure since they are differently shaped. Kids work on ideas in groups, while the teacher circulates to select some ideas varying from the most common to the most problematic to the most creative. The various groups send representatives to present their ideas to the class, there is much discussion, and at the end of the lesson the teacher will begin to present written, conventional forms of the math involved: in this case, a bar graph. Often students are then asked to come up with their own related problems to present to the class.
Another model is the Marilyn Burns classroom ( http://www.mathsolutions.com ). Most “lesson replacements” or sessions in the booklets begin with an activity: making, drawing, building, using manipulatives, reading a math picture book. As with the Japanese model, the lessons work towards written representation through much discussion and different problem-solving approaches. Algebraic thinking — pattern-finding, pattern-making, etc. — is introduced very early on, as is geometry, through geoboards, pattern blocks, and other manipulatives. Arithmetic is always part of how you work on the activities or problems, but it is never rote. Practice comes in other forms, and kids in a classroom could presumably choose from worksheets, flash cards, games, using an abacus, a calculator, etc. or rotate among these.
Applied math is sadly lacking in most early science programs. Although my daughter didn’t care much for the scripted approach of TOPS science, it did involve a lot of graphing, and there are some great units on measurement and scale. GEMS has some fun units on math, including a great one called Build It Festival. My daughter was so infatuated with the square meter we built from rolled newspapers that she made it into a tent and played in it until it collapsed. Activities like these could be incorporated into more traditional LB math classrooms as well (but not with the current pressurized testing-driven curriculum).
Tossing around right-brained ways of sharing math, Karen, always gets me thinking. The trick to me is how to integrate the right-brained methods, while still maintaining the left-brained ones for those learners…if both learners will be in the same classroom. So, for instance, one thing I didn’t like doing was working in groups. When it came to learning, I much preferred to work alone. So, if a problem is presented as you shared, then the option to work together or alone could be offered.
The other thought is that I like to work from filling out those worksheets, and then showing you maybe that I know what that looks like in concrete form. Your examples are working in favor of right-brained children who need to see how it works, and then the teacher can translate, and then they can work some problems. Mine would need to be the opposite, Though tricky, I think both can be accommodated if more space is allowed for independent learning.
So, instead of a teacher-down model of learning, it can be a “subject space learning model.” So, math time is for an hour, and there can be centers maybe with different ways of learning the concept. Math worksheet at one table with manipulatives to show you understand. Building manipulatives or abacuses at another table to play around with a concept, and then an interpretation model. Another table could have a written story that showcases a math concept, and then a student can draw out, act out, or mentally share what they know, then interpret.
That’s where having volunteers would come in handy…manning different tables as the teacher rotates. Ideas to toss around, huh?
Every time I read one of your articles, I get new thoughts. Thank you for this website!
I realize that I still struggle with wrapping my brain around left-brain thinking. Over and over, I kept thinking, “But what is the point of learning a bunch of methods if you don’t understand how or when or why?” But just as unschoolers often must trust (and/or encourage others to trust) that skills will come with time and development, my difficulty is in trusting that concepts will come with time and development — at least as much as is necessary to make use of necessary skills anyhow.
I still see most of these ideas through my work and my children. Since my work was with adoloscents and my children are 7 and under, I am missing the middle part of the picture: the 8-12 range.
I also realize that looking at dominance in learning from an adult (my) point of view is different, because the corpus callosum (the path that joins the two hemispheres of the brain) is already developed, AND left-handers have a thicker corpus callosum, allowing more talk between the hemispheres and perhaps thoughts and behaviours that appear more ‘whole-brained.’ In addition, just as in the studies showing that while musicians started off their early training using primarily their right brain while playing music, career musicians use both sides of the brain while playing music, I conjecture that a similar pattern occurs in other professions.
I will address your first question:
This is an excerpt from a more private blog of mine: “K. also makes more sense to me now. From the beginning, I thought of him as a creative, divergent thinker. Imagine my surprise when he began to take to numbers at 3 or 4 years of age. He understood fractions quite as quickly as A., the basics anyhow, and had the general idea of ‘negative’ (numbers) while A. was learning them — K. was 2. … he loves puzzles (which I considered left-brained), building, experimentation (I also considered this left-brained), art, cooking, and all the other right-brained activities …”
My son (K.) loves to play with the fraction manipulatives we made. He sells or eats pies and cakes. He throws numbers into conversation in a way that gets people to show them how those numbers fit into that context. He loves games. We play three-in-a-row-type games, chess, integer beans, Monopoly. He counts. Everything. And nothing. His pattern block designs are counted out and planned in his head before execution. They are usually symmetrical, laterally or radially. He is obsessed with designing and cutting snowflakes. He builds pyramids out of paper, Lego, anything he can get his hands on. He explored the different types of pyramids.
My daughter is more scientifically inclined, but she is also interested in math. Her interest and enthusiasm are mainly what tells me she has some ‘math mind.’ She does arithmetic in her head, rarely on paper. She loves math fiction. She discusses bigger concepts, like the different levels of infitinity. She learned to understand and manipulate integers before she was proficient with subtraction.
Cindy, I love your idea of using portfolios as assessment tools, and the graphic rubric that goes with it. The rubric is tangible enough that it could pass from teacher to teacher without losing meaning — well, not much, since subjective evaluations always lose something when they get passed on.
Lots of thoughts going through my mind with your thoughts, Victoria. First, this one: “skills will come with time and development, my difficulty is in trusting that concepts will come with time and development — at least as much as is necessary to make use of necessary skills anyhow.” When children are in their foundation years, I think we do have to trust that the way they prefer to learn at the outset will work in the other half as they integrate AND if it becomes important to them. Obviously, we would want to have learning both ways available, I think, like the center idea I stated above. What do you think of that?
Where did you get the information about left-handed people having more connections. I think I just heard somewhere…don’t remember where now…that there are more connections for those who multi-task (i.e., women).
I love the examples you were able to share with how your son interacts with math. Because he talks about numbers so much, one would suspect being left-brained, but HOW he talks about it and WHAT he focuses on may very well show how right-brained he is in his math thinking. Isn’t that quite cool!? I think that’s the tricky part to describe to people…how the math/numbers creative outlet looks in a right-brained learner. It’s definitely not the same as my excitement over filling out a worksheet of problems.
My highly verbal artist son was my only mental math person, especially at a young age. Is yours also highly verbal and/or gifted? Just looking for a correlation… If Life of Fred had been around for my oldest, I would be curious if he would have liked it. I’m thinking quite possibly.
Again, thanks for the current insights as you observe your children and record it for those of us to think about. Quite fascinating to me…
“When children are in their foundation years, I think we do have to trust that the way they prefer to learn at the outset will work in the other half as they integrate AND if it becomes important to them. Obviously, we would want to have learning both ways available, I think, like the center idea I stated above. What do you think of that?”
Of course. That learning to trust is such a process, particularly when the way forward is so murky. Knowing other’s experiences and seeing patterns laid out — like they are on this site — help a lot. The center idea sounds good. It seems a bit overwhelming to think of creating all of these centers when my experience tells me the curriculum might be changed in the following year. At the same time, if it can be set up for Language Arts, why couldn’t it be set up for math? But, I think it would be difficult for a solitary teacher to set up his or her class this way in a school that was still teaching the ‘usual’ way in all the rest of the classrooms. Maybe not, not at the elementary level. This is getting away from my area of expertise.
“Because he talks about numbers so much, one would suspect being left-brained, but HOW he talks about it and WHAT he focuses on may very well show how right-brained he is in his math thinking. Isn’t that quite cool!? ”
That is interesting how that came across. My son is not naturally a talker. In fact, he has always been “the quiet kid with a mission.” But his sister does influence him! She is highly verbal and probably gifted — and talks constantly. I do think that it’s cool that how and what my son focuses on shows how right-brained he is. With math, at least, he stays on topic more or less. Everything else, he tends to veer off onto wild tangents. On other planes. I wonder often how homeschooling him will unfold as the years go by.
“Where did you get the information about left-handed people having more connections. I think I just heard somewhere…don’t remember where now…that there are more connections for those who multi-task (i.e., women).”
I’ve heard the bit about multi-tasking recently too. The information about left-handed people, oh, that would have been out of one of my professional development books in the late ’90s. Sorry, I don’t remember which one.
I’m enjoying these discussions. Very interesting indeed.
I love getting to discuss my ideas with a teacher so I can see what may or may not be feasible based on the needs I see with particularly elementary aged creative learners. Well, I started to directly reply about the math center idea and it got long, so guess what? I’m going to try to do a “Teacher Talk” post every couple weeks or so about an idea for the classroom to get some discussion going among teachers, hopefully. That will be my first one, so stay tuned! I love comments because they create great fodder for more posts for more discussions!
My first two children became best friends, and I’m wondering if it was because they were such opposites that they complemented one another. I totally noticed that they each subconsciously encouraged through modeling the other in each of their own interests and styles of learning because they liked being around each other and would pick up from each other. So, like you saw, my oldest artist son was my talker/gifted one and he was always talking about his history stuff he liked around his younger sister. She was not one who naturally liked history, but she picked up a lot because she always heard him talking about it. She also picked up drawing from him because he was always drawing. As an adult, she is totally a competent drawer, though you wouldn’t call her a natural artist, but she developed her own interesting style that totally works, and she’s good at it. On the flip side, my highly right-brained oriented artist son would actually try a workbook page from time to time because he saw his sister so into them from time to time herself. Her focus made him want to try it out to see what all the interest was about. It didn’t last long, but he tried…haha!
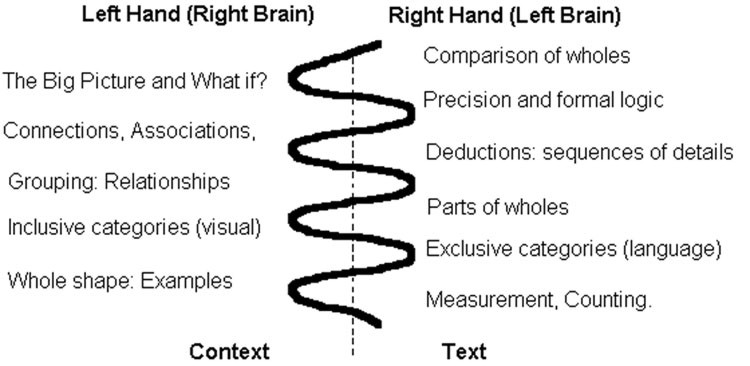
Pingback: Teacher Talk: Math Corners | The Right Side of Normal